統計解析R 入門講座 vol.4 〜 基礎統計量を求めよう〜

By terada, 2016年7月30日

前回は統計学で最も基本となるヒストグラムの描き方をご紹介しました。あるデータの集まりの特徴をつかむためには、ヒストグラムはとても強力なツールとなります。しかし、ヒストグラムから見て取れる情報は、データの概観だけであり、正確な特徴をつかむことはできません。そこで、ヒストグラムの特徴を数値で表す統計量というものが存在します。ここではその中でも、もっとも重要と言ってもよい、平均・分散・標準偏差を求めてみましょう。

まずはデータのヒストグラムを描いてみよう

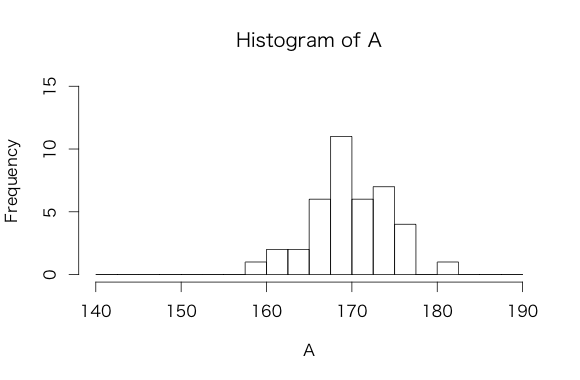
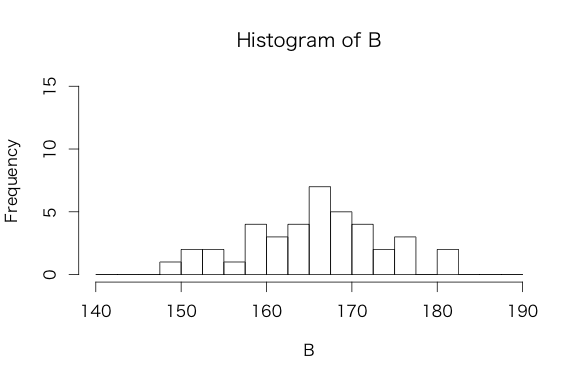
例題として、ある2つのグループの身長がデータとしてあるとします。グループA、グループBのそれぞれの人の身長は次の値であるとき、まずはそれぞれのヒストグラムを描いてみましょう。

グループA

168.7	169.4	170.1	176.0	174.9	169.6	172.4	167.7
161.9	168.1	166.5	167.9	170.0	174.7	177.2	172.9
167.4	169.7	171.5	176.1	167.4	159.8	168.8	176.7
162.3	170.6	165.8	171.5	165.4	181.9	164.4	172.9
173.3	174.4	170.4	169.6	166.6	169.3	164.4	174.1

グループB

167.5	171.4	166.3	166.6	161.7	168.9	150.4	149.0
163.9	159.7	172.8	167.7	152.3	170.5	172.3	168.6
156.5	175.1	180.6	175.0	164.2	163.2	165.3	168.8
166.1	162.0	181.2	170.3	163.2	167.2	168.0	154.7
159.9	176.2	158.9	158.2	165.4	154.1	176.1	162.1

それぞれのヒストグラムを描くためにはRで配列を作成する必要があります。この例では”c”というコマンドを使ってそれぞれの配列を作成しています。配列の作り方は色々種類があるあります。中には数値を選択・コピーして貼り付けて配列を作成できる”scan”という関数もあるので用途に応じた使い方をしてみてください。

#グループA
A = c(168.7, 169.4, 170.1, 176.0, 174.9, 169.6, 172.4, 167.7, 161.9, 168.1, 166.5, 167.9, 170.0, 174.7, 177.2, 172.9, 167.4, 169.7, 171.5, 176.1, 167.4, 159.8, 168.8, 176.7, 162.3, 170.6, 165.8, 171.5, 165.4, 181.9, 164.4, 172.9, 173.3, 174.4, 170.4, 169.6, 166.6, 169.3, 164.4, 174.1)

#グループB
B = c(167.5, 171.4, 166.3, 166.6, 161.7, 168.9, 150.4, 149.0, 163.9, 159.7, 172.8, 167.7, 152.3, 170.5, 172.3, 168.6, 156.5, 175.1, 180.6, 175.0, 164.2, 163.2, 165.3, 168.8, 166.1, 162.0, 181.2, 170.3, 163.2, 167.2, 168.0, 154.7, 159.9, 176.2, 158.9, 158.2, 165.4, 154.1, 176.1, 162.1)

# ヒストグラム描画
hist(A, breaks = seq(140, 190, 2.5), ylim = c(0, 15))
hist(B, breaks = seq(140, 190, 2.5), ylim = c(0, 15))

さておそらく上図のような２つのグラフが描けたかと思います。ヒストグラムを見ることで、それぞれのグループの特徴を大まかにつかむことが出来ます。特徴としては、

• どちらもデータの中心の度数が高く身長が低い/高い方に行くほど度数が少なくなる
• グループAの方がグループBに比べて中心が少し高い値にありそう
• グループAの方がグループBに比べてデータが中心に集まっている

などです。ヒストグラムを見ただけでこれだけのことがわかるのですが、さらにこの違いを数値で表してみましょう！

統計量を求めよう

ではどのような数値で違いを表すのでしょうか。統計の世界では、データの中心を表す数値として平均、データのばらつきを表す数値として分散・標準偏差という値がよく用いられます。それぞれRでは次のように計算してください。

# 算術平均
mean_A = mean(A)
mean_B = mean(B)

# 分散(不偏分散)
var_A = var(A)
var_B = var(B)

# 標準偏差
sd_A = sd(A)
sd_B = sd(B)

平均は”mean”、分散は”var”、標準偏差は”sd”という関数で計算することができます。平均は全てのデータの値を加算して、データの数で割ったものです。分散はデータの平均値からそれぞれのデータがどれくらい離れているかを表した値です。すべてのデータに対して平均値を減算して2乗し、その値の平均値を求めると分散になります。標準偏差は分散の平方根をとった値です。計算した結果は次のようになったと思います。

> mean_A
[1] 170.0575
> mean_B
[1] 165.5475
> var_A
[1] 20.9661
> var_B
[1] 59.88153
> sd_A
[1] 4.578875
> sd_B
[1] 7.738316
> 

グループAとBでは、平均で約5 cm、分散で40 cm² 、標準偏差で3 cmの差があることがわかります。このように、ヒストグラムだけではなんとなくの違いしかわからなかったことが、平均・分散・標準偏差という統計量を計算することで、数値で違いを表すことができるのです！これが統計の最も大事な部分の一つで、数理的にデータを解析するということです。

Rを使った統計解析の手順がなんとなくわかってきましたでしょうか？不定期ですが続けてR入門講座を書いていこうと思います。それでは次回をおたのしみに！

Soraotoでは社会人・大学生向けに、「統計がイマイチよくわからない人のための統計講座　〜Rで覚える統計の基礎〜」を行っております。内容は「記述統計編」「推測統計編」「相関・回帰編」の全3回をR言語を使って学びます普段統計に馴染みのない方から、仕事や学校で統計が必要な方まで、ぜひ受講してみてください。

Soraotoの統計講座 (http://www.soraotona.net/english.html#statistics)
詳しい開催日程は、当ブログ、Facebook、Twitter等で告知いたします。